[Original Software] EMail Address Collector
A software used to collect or extract mail address from web.
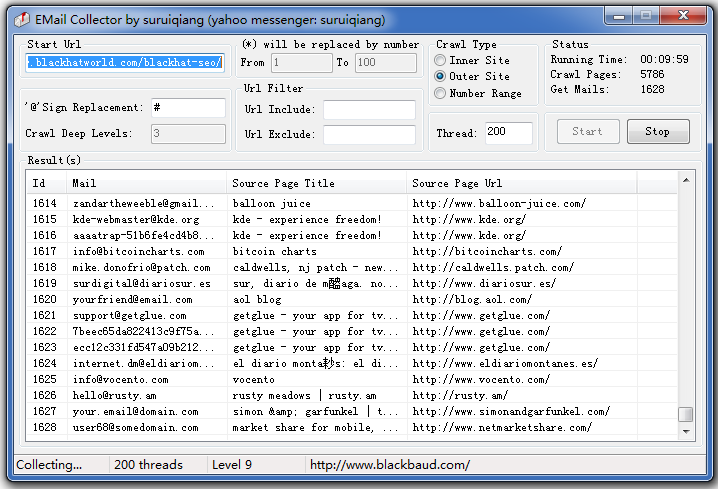
1.This software doesn’t depend on search engines(My another software that can collect email from search engine will be published later), It crawl web from start URL.
2.Users can specify the replacement sign of email (for example some site use # instead of @ in mails).
3.Users can specify the deep level to crawl.
4.When it is crawling, you can control the crawl direction using include filter and exclude filter.
5.It can collect mails from single domain (Inner Site Type) or cross-domain (Outer Site Type).
6.It can easily collect mails from urls including continuous digit.
eg: type “http://www.abc.com/thread.php?id=(*)” as start url, set the number range from 1 to 100, then the read url to fetch is:
http://www.abc.com/thread.php?id=1
http://www.abc.com/thread.php?id=2
http://www.abc.com/thread.php?id=3
…
http://www.abc.com/thread.php?id=100
[Original Software] EMailSpliter, A Tool for sorting emails [Original Software] EMail Scraper From Search Engine
Hello, how can i download the original software of the this.. waiting for your reply
You can download on this page directly.
I want to pay for this softwares how will i pay?
EMail Address Collector
Smtp cracker update to v1.1
EMailSpliter, A Tool for sorting emails
i want to buy the original software for mail colector ans smtp scanner. please how will i make the payment because i have a paypal account. lisa
sent u an email
please check
ok
check your email and update me lisa
replied
i wan to buy email from you company email such as importers and exporters from alibaba
replied your email
please check
by the way, i only sell softwares i don’t sell email leads,smtps or other data since i am a programmer not a spammer
thanks
Hi Bro,
I just sent you a mail please i need you to update me on the prize of the email scanner and smtp cracker.Please check your email i also sent you a friend request on ym.
thanks
I think i have talked to u on yahoo messenger
I need the prize for the email collector and the SMTP mail cracker.Please check your email and reply me because i need both ASAP.
Thanks for the good job bro.
I think i have talked to u on yahoo messenger
Please send me an email no your payments fee for the EMail Address Collector.
Awaiting,
Amaga Sam.
just email me
suruiqiang@msn.com
Pls email me software and payment details asap
Briggs
sent u an email
pls check
Please what is your email?
hello
my email is suruiqiang@msn.com
Do you have software for cc collector ?
hello
sorry i don’t have cc collector.
Please after email collection with the ”Email collector” how do one bring out the emails collected from the software, anyone should help please.
i have replied your email
please check
Sanmoa, please send me your email with your email address to resultbaze@gmail.com, I added you with suruiqiang but have not seen you too talk to, contact me please
i have seen your email and i have replied it
please check
Sama can you build smilar software for collecting emails so we can generate with your url link generator and load the Url instead of single url if you can do that for me add me on whatsapp for chat +140(*)8668
current email collector can get emails
Hello,
How do i save the emails after the program finish the search?
I need to buy the license?
Thanks
hello
sent u an email
please check
please what kind of domain leads do i use and how do i get the domain leadson the sanmoa smtp cracker,hope to hear from u soon
hello
if u have any question, just add me on yahoo messenger or skype or send me an email
I want this software EMail Address Collector,what is the cost ?
email collector is $20 for one pc license $40 for unlimited pc license
i just add you to my yahoo messager list with this ID:c_claims0020
added u on YM
I need to buy latest sanmao smtp cracker pls send me payment method i need it urgent
we have talked on YM
I just added you on YM, i want the email collector for multiple pcs.
talked with u on YM
Hello i’m wondering if your software working on Apple Macetosh?
i am sorry
my software can only work on windows system for now
they can’t run on mac os x
if u have a apple computer, u can install a vm
please can the trial version save emails ?
trial version can only show results on the software, it can’t save the results to a file
that’s the only difference between trial version and full version
Am having problem with Email Cracker, please i have talk to you already on Yahoo messenger, kindly give me a feed back
what problem do u have?
i have left u messages on YM
I want to purchase the email collector. How much is it ?
the email collector is $20 for one pc license $40 for unlimited pc license
I want the email extractor latest version. How much does it cost ?
i have sent u an email
Pls how can I buy
i accept these payment methods:
perfect money
skrill
webmoney
bitcoin
payza
western union ($50 or more)
moneygram ($50 or more)
I want to purchase email collector
i have sent u an email
please how do you query the email collector using url..its very difficult…please help ..show some sample on how to do it
there is how to get the start url in the collector’s video demo
u can watch the video demo
how do i copy out the emails from the email collector software
trial version can’t save result to file
the full version auto saves results to file
that’s the only difference between trial version and full version
pls I want to buy email collector ,hope it can extract ceo email leads?
email collector is $20 for one pc license $40 for unlimited pc license
not only ceo emails
all kind of emails
hi
how can i get this programme and how can i pay for get it and buy it
are thear bro ?
my online time range is 9:00AM – 6:30PM every day
my timezone is GMT+8
china time
please send me email if u want to buy it
email collector is $20 for one pc license $40 for unlimited pc license
what the diferent between them
my email is sem(*)100@gmail.com
different between what?
ok i have seen your email and replied it
okey i want to buy it 🙂
i want buy email collecteur and i want buy smtp cracker how much you can sell me this 2 application
sent me email please
suruiqiang@msn.com
Hey bro, please reply my email.. I sent you a mail earlier today.. Need to know which one to buy.. Thanks..
i have replied your email
please check
I want to buy your SMTP Mail Cracker
ok
just seen your email
replied it
DO YOU SELL RDP ,OR WHERE CAN BUY BUY?I NEED SOME ONE I CAN TRUST LIKE YOU
i don’t sell rdp
and i don’t know one good rdp seller
Please i need this software used to collect or extract mail address from web. list your payment method to me and how much does it cost?
email collector is $20 for one pc license $40 for unlimited pc license
i accept these payment methods:
perfect money
bitcoin
payza
worldremit
Good day Sam
I need the Email Collector and Email Scraper.
I sent you an email,please check and get back to me.
okay
replied it
pls forward your pm account to me for payment
my perfect money account is U1548452
after u send the pm
please send the batch number to sanmaosoft@gmail.com
once i receive it i will send u the download link of software immediately if i am online
and if i am not online i will send u it next day
my online time range is 9:00AM – 6:30PM every day
my timezone is GMT+8
I need this software ASAP
okay
email collector is $20 for one pc license $40 for unlimited pc license
i need the email collector….. how does it work?
about how it work
u can watch the video demo
I need the email collector
one pc licence
we have talked in email
Yes.
Credited
How much is EMail Address Collector
email collector is $20 for one pc license $40 for unlimited pc license
How much is EMail Address Collector and URL Link & Domain Collector, Send me Your PM number for payment.
https://www.sanmaosoft.com/?p=67
https://www.sanmaosoft.com/?p=396
email collector is $20 for one pc license $40 for unlimited pc license
the url collector’s price is $30 for one pc license $60 for unlimited pc license
send me your PM number for payment.
let’s talk via email
Also for EMailSpliter
spliter is free
How much is the email collector?
email collector is $20 for one pc license $40 for unlimited pc license
i want to buy this email address collector. i would like to know how much it cost.
do you sell RDP one that i compact-able with the address collector ?
email collector is $20 for one pc license $40 for unlimited pc license
i don’t sell rdp
local pc is ok for collector
i need email collector asap. kindly contact me with details
okay
u can email me too
Please do you accept paypal and is there a place I can chat with you ?
Thanks
i accept these payment methods:
perfect money
bitcoin
bitcoin cash
ethereum
payza
worldremit
i don’t accept paypal
u can contact me with email, icq or skype
i want to make payment on your EMail Address Collector
okay
just email me
Hello! I will be needing multiple programs from you. I sent you an email for one of your programs but I actually need information on quite a few of them. I will email you once more for which programs I need. Thanks!
saw your email and replied it
please check
hi pls your demo video are not clear at all as i cant see clearly to follow the instructions on how to use the app email collector and your smtp cracker can you please email me instructions on how to use it or better still make a more clearer video and upload thanks
it’s HD video
on youtube u can change the video’s quality
Hi, how can i buy it?
email collector is $20 for one pc license $40 for unlimited pc license
What is the difference between this email collector and your email scraper ?
Which one is better than other ?
“email collector” is “crawl” type, u set a start url, it will crawl from here, then crawl into its links and extract emails on these pages, then crawl into link’s link
“email scraper” is “search” type, u load some keywords, it will search every keyword from search engine, then extract emails from search result page.
i don’t think there is a “better” one and a “worse” one (many people ask me, which one is better)
because they are different type
someones like the first one, and someones else like the second one
u can download both of their trial version to check which one is suitable for u
I need your email address so that I know whom am dealing with. To know if the one I had is the real Samoa
2ndly if I pay today for the smtp v1.7.1 cracker 50pm when will I get it
my email address is on the top of current page
I want this email collector and also reply your email and chat on icq
i have replied all messages i got
what is your icq id?
I want the email extractor latest version, EMail Verifier / Validator and Roundcube CPanel Email Judger v1.0.4. How much will it cost ?
contact me please
HOW DO I GET THE EMAIL EXTRACTOR
contact me please
Hello Sanmao,
I want to buy the full version of the software. How do i buy it and how much?
thank you
okay
contact me please
i need email collector and mail cracker
okay
contact me please
price
email collector is $20 for one pc license $40 for unlimited pc license
What is the latest version of this email collector?
no update recent year
wrote you on tg but no answer. How can I contact you for purchase?
where did u send msg to?
Hello, I need the smtp creeker and scanner.
Please contact us through the contact information page
Is this tool still working?
And why you have not updated it?
Yes, working